THE AVERAGE reader—as distinct from the science-fiction reader—has had a number of terminology problems during the past few years. His favorite newspapers and magazines, instead of talking about things one could understand like sad-eyed puppies and clean-cut little boys who, unfortunately, are too stupid to spell properly, has started talking of orbits, perigee and apogee, inclination to the equator and similar things. Quite a number of people are convinced that these are all brand new words, invented either in Washington or in Huntsville, Alabama. In reality they are standard astronomical terms that have been around since the early part of the seventeenth century.
But recently talk about L-points has started and though this, too, is a standard astronomical term, I suspect that not even all science-fiction readers are quite sure just what an L-point is.
To begin at the beginning, the L stands for Lagrange, full name Joseph Louis Lagrange, who lived from 1736 to 1813. Lagrange was a mathematician with strong astronomical leanings, and as his name indicates he was a Frenchman. Frenchmen have the reputation of being people who stay home, or at least in France. If this is truly a national characteristic of the French, then Lagrange was an atypical Frenchman. To begin with, he was born in Torino, or Turin, in Italy and was educated there; he also had his first position in Italy, being appointed (at the age of nineteen!) professor of mathematics at the Artillery School at Torino. While engaged in the task of hammering some mathematics into the skulls of future artillery commanders he corresponded with the mathematician Leonhard Euler and laid the foundation for the branch of mathematics which later came to be called calculus of variations.
At the age of 28 he published a mathematical treatise on the motion of the moon which was awarded a prize by the French Academy of Sciences. Two years later, he followed up with a theory of the motions of the satellites of Jupiter which made such an impression in Berlin that Frederick the Great of Prussia appointed him director of the Berlin Academy of Sciences. Lagrange spent the next twenty years of his life in Berlin until, finally, in 1787 Louis XVI of France invited him to come to Paris. There he spent the rest of his life, heading a commission for the reform of weights and measures, being professor at the Ecole Polytech nique and finally becoming a senator and elevated to Count by Napoleon I.
During his investigation of the orbits of our own moon, as well as the orbits of Jupiter's satellites, Lagrange encountered a problem which he did not solve: the so-called three-body problem.
THE PROBLEM is very simply this:
Assume three bodies in space—say a planet which has two very large moons in orbit around it. You know the mass of every one of these three bodies. You also know their relative positions, and you know their orbital velocities at this moment. Now find a set of simple and elegant equations which permit you to predict the future motions of these bodies, accounting for their mutual attractions all the time.
Lagrange tried hard, but failed; and to this day nobody has been able to come up with such a set of equations.
Of course we can and do calculate such cases—for example, when it comes to predicting the motion of a comet. But it has to be done by way of endless step-by-step calculations which have to be checked against observations all the time.
But, while Lagrange failed to find an overall solution of the three-body problem, he did find a number of special cases where there was a solution, provided the bodies were in certain relative positions to each other. In fact, there were five such positions ... which later were called the Lagrangian points, or L-points.
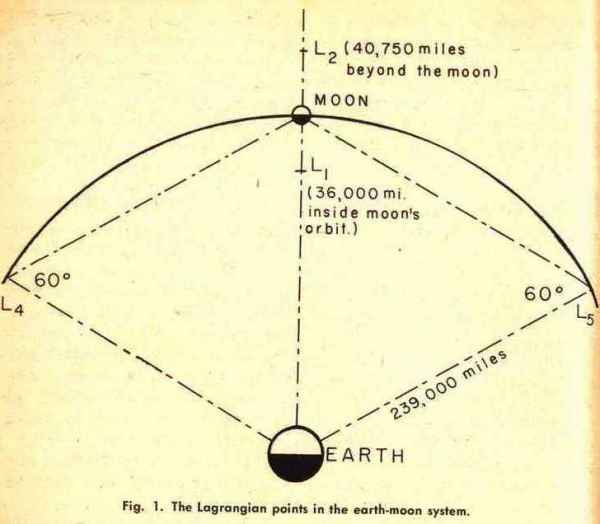
For an example of the Lagrangian points let us look at the earth-moon system. (Fig. 1.) The earth and the moon are two of the three bodies. The third one would be a hypothetical satellite; and the problem would be to find a position in which it would have an easily predictable orbit. Two of these points are the ones known as equilaterals, positions L-4 and L-5, where the satellite would travel in the orbit of the moon and would, of course, have the same orbital period as the moon.
But there are two more such points which lie on the line connecting the center of the earth with the center of the moon. One of these two is closer to us than the moon; the other is beyond the moon. Now, if our moon did not exist, a satellite moving at the distance of the L1 point—about 203,000 miles from the earth's center—and another satellite moving at the distance of the L2 point—about 280,000 miles from the earth's center—would have different orbital periods. The L1 satellite would need less time than our moon; the L2 satellite would need more time. But because our moon is there the satellites in these points would have the same orbital period as our moon.
One may try to visualize this by imagining that our moon's gravitational force drags the L2 satellite along a bit faster than it would move normally, and keeps the L1 satellite back so that it does not move quite as fast as it would by itself.
We now know that the L4 and L5 positions are actually occupied by dust clouds. The L1 point is not occupied, while an occupant of the L1 point could never be seen from earth. (In the future both the L1 and L2 points may be occupied by radio relay satellites, if we get more than one human settlement on the moon. Because of the fairly strong curvature of the moon's surface, two distant lunar bases could not have direct radio contact. But they could talk to each other easily via relay satellites, located in the L2 point for bases on the far side of the moon, and in the L1 point for bases on the lunar hemisphere which is visible from the earth.)
BEFORE I go on, one loose end and one possible misunderstanding have to be taken care of.
The possible misunderstanding concerns the L1 point. Everybody knows that, between the earth and the moon, there is a "neutral point", a point where the gravitational fields of earth and moon have the same strength. This neutral point is not the same as the L1 point. In fact it is closer to the moon, roughly 24,000 miles from the lunar surface, or about 25,000 miles from the center of the moon.
As for the "loose end", as I called it, it is the simple question "where is L3?" Well, L3 is also on the line connecting the earth and the moon. But it is on the other side of the earth, below the bottom of our diagram.
Now, these Lagrangian points exist for every planet and its moons. They also exist if you consider the sun and a planet the two bodies. In other words, we could have equilaterals in the earth's orbit and in any other planetary orbit In the case of Jupiter the equilateral points are known to be occupied, both the advance and the trailing position.
Quite recently Dr. W. B. Klemperer has done some more work on the three-body problem. Like Lagrange he failed to find a general solution, but he succeeded in extending Lagrange's special cases, which always dealt with three bodies—though of course all the L-points around one planet might be occupied—to special cases of many bodies.
You can have stable systems for three, four, five, six, eight and so forth bodies. They have to fulfill two conditions: they must orbit in the same plane; and they must, at any moment, form a regular polygon. Whether there is a major mass in the center of that polygon or not does not matter; the orbits would be stable with or without a central mass.
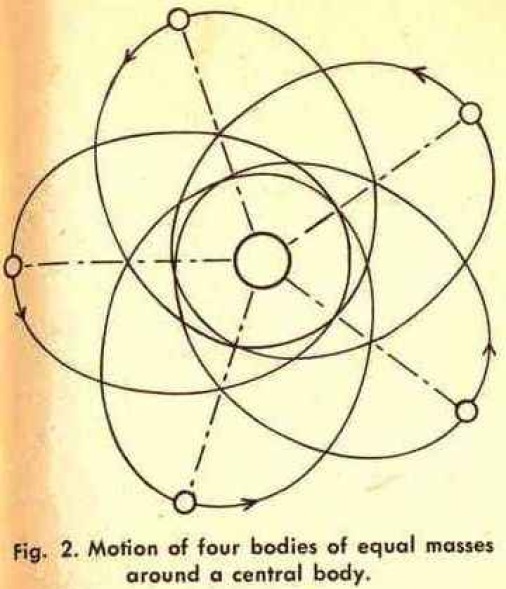
One such possible arrangement is shown in the second diagram. Here we have four bodies, orbiting in the same plane and in elliptical orbits of the same size and eccentricity. The open circles show the four bodies at their extreme distances from the central mass (which needn't be there) and they form a square. Some time later, all four bodies have moved the same distance along their orbits, as indicated by the closed circles, and they still form a square. This system would be stable. So would the five-body system shown in Fig. 3. And a 64-body system, forming a 64-cornered regular polygon, would be stable too.
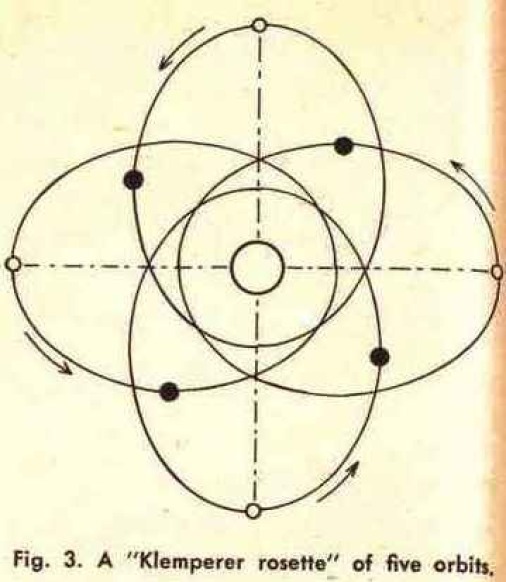
I said a short while ago that two conditions must be fulfilled: the bodies must form a regular polygon at any moment and they must move in the same plane. Do they also have to have equal masses, as indicated in the diagrams?
The answer is that they do not have to have equal masses, provided another condition is fulfilled. If we had a six-body system, forming a regular hexagon, the bodies could be of two different masses, but then they would need a regular arrangement. The larger and the smaller bodies would have to alternate. In the hexagonal system, bodies 1, 3 and 5 would have to have the same mass and bodies 2, 4 and 6 also would have to have the same mass. But bodies 1, 3 and 5 could be five times as massive as bodies 2, 4 and 6.
These interesting arrangements would not last if an additional body wandered into the system from the outside. For this reason it is not very likely that such systems actually exist.
But it would be careless to proclaim that they do not exist. When Lagrange theoretized equilaterals back in 1772 no actual case was known, and because of such lack of confirmation in nature his "points" were very nearly forgotten. But then asteroid 1908-TG was discovered by Max Wolf in February, 1908, and when the orbit was computed it was found to move in the orbit of Jupiter. Its running number and name became 588-Achilles and it was the first equilateral found.
Maybe a "Klemperer rosette" will turn up, too!
— WILLY LEY





Click to join 3rdReichStudies

Disclaimer:The Propagander!™ includes diverse and controversial materials--such as excerpts from the writings of racists and anti-Semites--so that its readers can learn the nature and extent of hate and anti-Semitic discourse. It is our sincere belief that only the informed citizen can prevail over the ignorance of Racialist "thought." Far from approving these writings, The Propagander!™ condemns racism in all of its forms and manifestations.
Fair Use Notice: The Propagander!™ may contain copyrighted material the use of which has not always been specifically authorized by the copyright owner. We are making such material available in our efforts to advance understanding of historical, political, human rights, economic, democracy, scientific, environmental, and social justice issues, etc. We believe this constitutes a "fair use" of any such copyrighted material as provided for in section 107 of the US Copyright Law. In accordance with Title 17 U.S.C. Section 107, the material on this site is distributed without profit to those who have expressed a prior interest in receiving the included information for research and educational purposes. If you wish to use copyrighted material from this site for purposes of your own that go beyond 'fair use', you must obtain permission from the copyright owner.
Sources: Two superior Yahoo! Groups, magazinearchive and pulpscans, are the original sources for the scans on this page. These Groups have a number of members who generously scan and post rare and scarce magazine and pulp scans for no personal gain. They do so for love of the material and to advance appreciation for these valuable resources. These Groups are accepting new members; join now!